An innovative, game-like tool to learn chemical and chemical engineering concepts designed for pupils younger than 14 years – how could that look like? Well, we don’t know that precisely yet. But definitely, there are other educational (or serious) games which could serve as examples how educational value is coated in a game which is actually fun! One of those examples is the algebra learning app Dragon Box 12+ developed by the software company WeWantToKnow, which I would like to introduce to you in the case of an educational mathematics game. I highly believe that one could be inspired how to set up and design a serious game for a young target group! (MD, Leuven, 10/02/2020)
Dragon Box 12+ is an educational app for iOS and android to become familiar with algebraic equations and the correct transformation rules [1]. What instantly stands out are the graphics. Child-oriented, colorful, hand-drawn and with a lot of attention to detail. It just looks great! For sure, the first puzzle-piece of the great effort put into the game.
You start with choosing one of more than 20 avatars to create your first profile and immediately you begin with the first of 10 chapters. Each chapter has 20 levels, each level can take from seconds to several minutes to solve it correctly, depending on your experience. At the end of the levels you are rewarded with 1 to 3 stars and a small growth animation of the dragon of the chapter. Each full grown dragon at the end features the design highlight and the most motivating element. You want to know what grows out there! Together with the growth of the dragon, you are also motivated to achieve maximum stars.
One of my favorite dragon designs from a self-made screenshot.
But what do you do actually? What are the game mechanics? And where is the math? So, essentially you see an area on your device screen with a box from which a dragon glimpses out, creature icons and other elements. However, the dragon only wants to come out and grow if it is alone in the area. You as the player are in charge to eliminate all elements around the dragon with gradually enhancing skills and abilities throughout the game. The math is exactly hidden here. We all remember from past classes, which entity also would, figuratively speaking, rather prefers to be alone. The variable x of an equation of course! And as in school, we gradually acquired more and more knowledge about algebraic transformations. So, the dragon in the box represents the variable x. All other elements like icons of other creatures and square numbers of a dice represent other variables and numbers as separate terms of an equation.
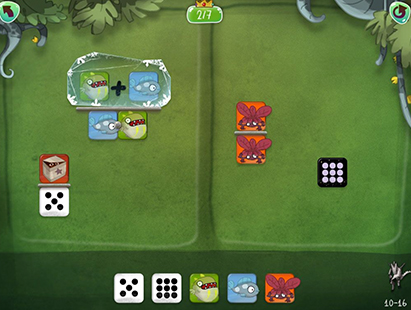
General look of levels at the symbolic creature icon state. [2]
Then, the gradually evolving skills shown in small animations represent new, more advanced rules for algebraic transformations. These are for example factorization, multiplication and division, simply mediated by tapping and moving icons as shown on screen. Typically, mistakes are done by pupils in school with not applying a multiplication or division to every single term on both sides of the equation. Here, the developers kept the game mechanics strict that you are forced to apply transformations to every icon on the field. No mistakes are possible there!
Another mechanic to eliminate icons on the screen, so that the dragon is alone, is introduced as icons of the same creatures in a bright and a dark color cancel each other. Keep your equation as simple as possible! If you don’t, even if the dragon is alone, you solved the equation technically correct but you can still simplify the other side. This results in a score of less than 3 stars. To make sure the aforementioned associations of the dragon in the box and the creature icons are made with algebra, the icons are replaced by variables and numbers gradually – already in the first chapter! With more progress, those symbolic substitutions are omitted and mathematical symbols like the equal sign between both areas are introduced.

General look of levels at the mathematical symbol state. [2]
If you play the game and see the associations with math directly, the game becomes easier. But for kids with no math knowledge, there is quite some challenge remaining. Fundamental algebraic laws like the commutative, associative and the dissociative properties are implied within the possible game mechanics, though they are not explicitly mentioned. Still the mechanics are simple, there is no need of further explanations. But if you need to recapture some mechanics/transformations you can always go back to a past chapter and beat your high score so far. Besides, a separate mode is unlocked as soon as you finish each chapter. Here, algebraic equations want to be solved straightforward. So in the end, you run through more than 200 equations – plenty of opportunity to practice new skills!
The appealing child-oriented icon and environment design makes abstract mathematical terms tangible. So I personally believe that even kids younger than 12 are able to play it and thus become far earlier familiar with algebra than before. In the last chapters, equations get fairly complicated and players have to set parentheses and summarize operations with common denominators cleverly to solve the equations in the requested amount of steps. An additional congratulations message pops up if you are even faster! To summarize: I can only highly recommend to give it a try! Besides its actual educational value it is a simple and amusing game as well!
But finally, I do not want to deprive that academic studies are also done on the effect on using Dragon box 12+ in mathematics education. The authors could show that the game can provide support for mathematics education of teachers in classes. However, since I wanted to present a personal point of view of the game in this scope feel free to have a look at the study yourself [3]. Although we are investigating game-like systems to teach chemistry, I am convinced that one could learn from this example what potential amusement lies in an educational game. Not without reason, the developers have won several awards and prices for their products so far [4].
References:
[2] https://dragonbox.com/products/algebra-12
[3] N. M. Siew, J. Geofrey and B. N. Lee, Students’ Algebraic Thinking and Attitudes towards Algebra: The Effects of Game-Based Learning using Dragonbox 12 + App, The Research Journal of Mathematics and Technology 2016, 5 (1), 66-79.
[4] https://dragonbox.com/about/press-and-awards